产品中心

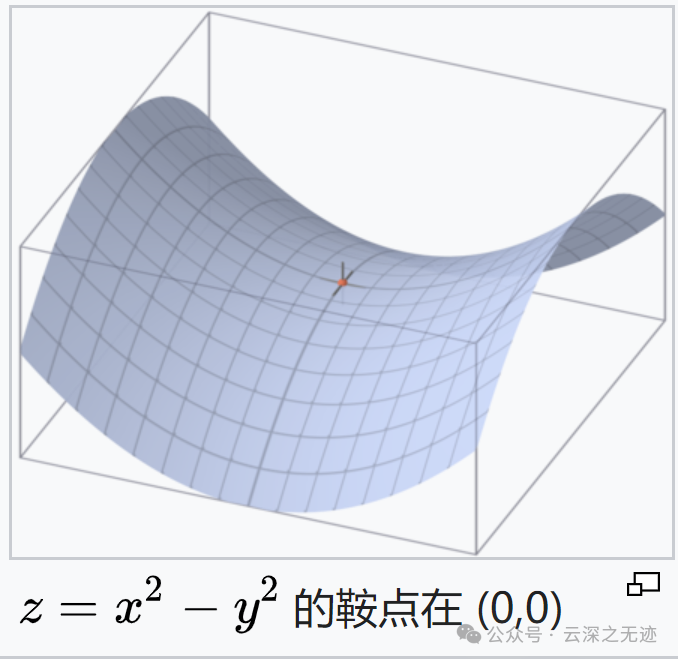
若曲线图形在一点由凸转凹,或由凹转凸,则称此点为拐点。直观地说,拐点是使切线穿越曲线的点。
若该曲线图形的函数在某点的二阶导数为零或不存在,且二阶导数在该点两侧符号相反,该点即为函数的拐点。这是寻找拐点时最实用的方法之一。
二阶导数不存在,无定义点,看这个点的左右两边。
拐点的必要条件:设f(x)在(a,b)内二阶可导,x0∈(a,b),若(x0,f(x0))是曲线y=f(x)的一个拐点,则f″(x0)=0。
比如,f(x)=x4,有f″(0)=0,但是0两侧全是凸,所以0不是函数f(x)=x4的拐点。
拐点的充分条件:设f(x)在(a,b)内二阶可导,f″(x0)=0,若在x0两侧附近f″(x)异号,则点(x0,f(x0))为曲线的拐点。
否则(即f″(x0)保持同号),(x0,f(x0))不是拐点。
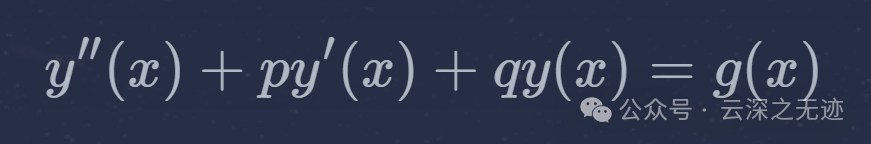
二阶常系数非齐次线性微分方程
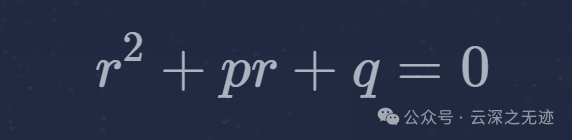
特征方程
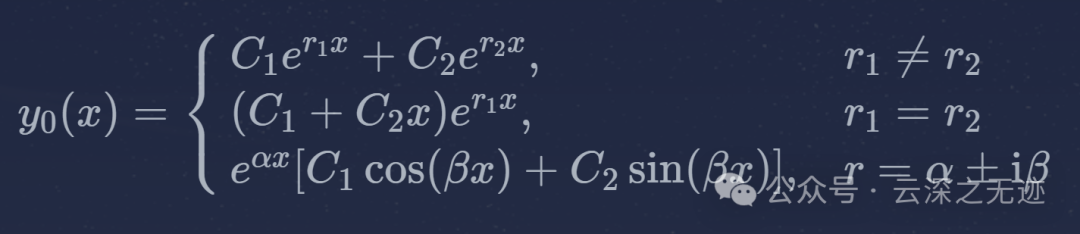
解的情况

在前面说过,后面的叫激励项,也会影响最终的结果,就是特解。现在可以给出结果的有下面这几种。

有时候我们看见题里面会有,设一个解的由来就在这里
方程里面的e的系数之间是线性无关的,也就是系数代表的项都为0.


上面这几个 PPT 也是对 e 无关的一个证明

补一个反比例函数,绘图有用
在绝大部分情况下,我们会使用θ作为外积分,r作为内积分;同时很容易确定二者的积分域:
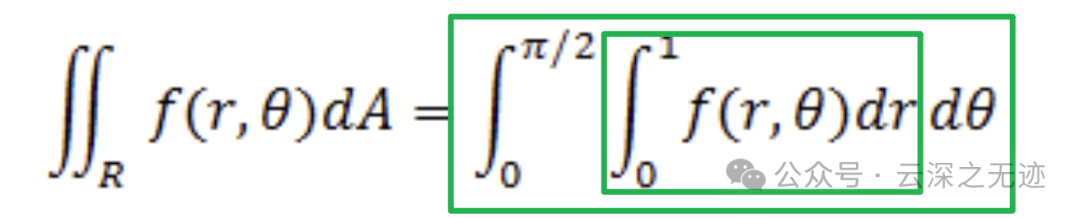
这个是重积分变成累次积分时候的次序问题
https://wap.sciencenet.cn/blog-39346-1287114.html?mobile=1https://blog.arg.pub/2021/10/12/math/%E4%BA%8C%E9%98%B6%E5%B8%B8%E7%B3%BB%E6%95%B0%E7%BA%BF%E6%80%A7%E9%9D%9E%E9%BD%90%E6%AC%A1%E5%BE%AE%E5%88%86%E6%96%B9%E7%A8%8B%E7%9A%84%E4%BA%94%E5%A4%A7%E8%A7%A3%E6%B3%95/index.htmlhttps://math.fudan.edu.cn/_upload/article/files/8b/6b/f3bc390143b09642a863057be4e7/0771b803-2e2b-487e-830b-a32e4e32dcfe.pdfhttps://www.cnblogs.com/Mount256/p/17502532.htmlhttps://www.cnblogs.com/Mount256/p/17502532.html